はじめに
こんにちは、品質管理部の沖です。
私は普段、製品に対する OS の影響を調査・検証する業務に携わっています。
業務において、製品の機能や製品によるデバイス制御の種別等、複数の観点による比較のために行と列が多重になった表を用いることがあります。
本記事では、このような表を一般化して捉え、簡易に作成するツールを作成しましたので紹介します。
また、ツールの本質的には表の出力ができれば十分ではありますが、マルチインデックスのハイパーキューブ描画もやってみました！
用語の説明
「通常の表」とその拡張であるマルチインデックスをもつ表、ハイパーキューブ、そして「通常の表」と「マルチインデックスをもつ表」の可視化のための別表現についてそれぞれ説明します。
「通常の表」とその拡張
- 行と列のインデックスをもつ「通常の表＝マトリックス」は一般に表計算等で用いられます 。
- 製品の機能比較等では、行と列がそれぞれ複数存在するような表を作成することがあります (図 1 を参照)。
- 複数行と複数列のインデックスをもつ表をここでは、 マルチインデックスをもつ表 とよびます。テンソル とよばれることもあります。
- 例えば、各製品の仕様を複数のOS・仕様に分類して比較する場合、表は単なる二次元の行列だけでは表現しきれないのでこのような表が必要になります。
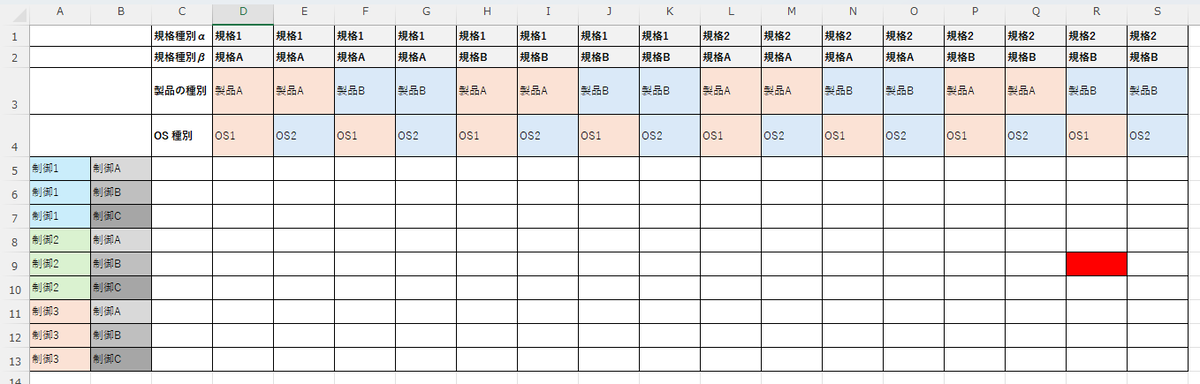図 1. 製品の機能比較の表
ハイパーキューブ
- 立方体を 3-cube とよびます。
- このとき、2-cube は正方形になり、1-cube は直線になります。
- 一般化して 4-cube, 5-cube, ..., 6-cube を考え、これらをハイパーキューブとよびます (図 2 を参照)。
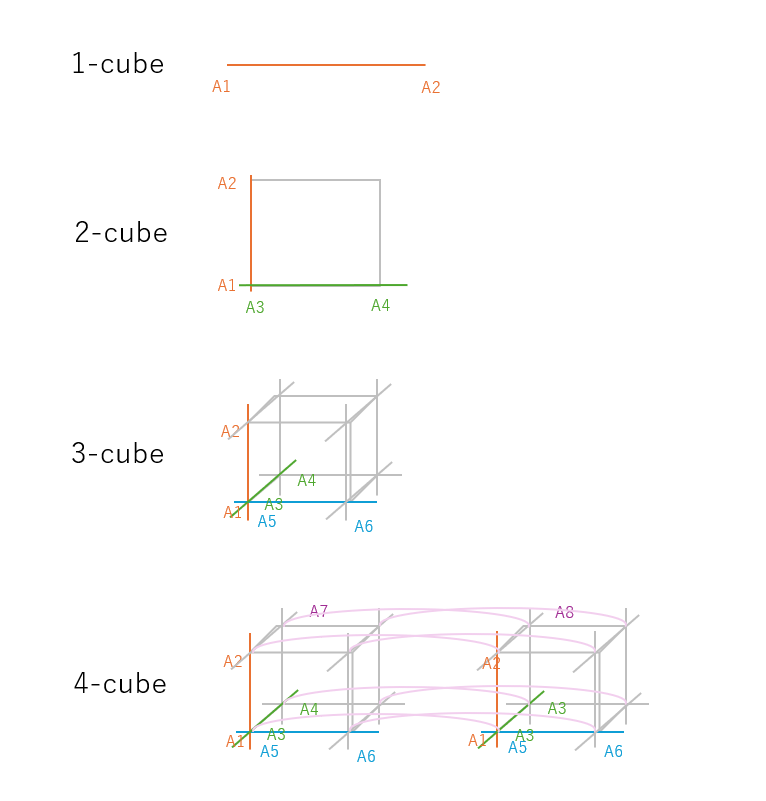図 2. ハイパーキューブ
「通常の表」の別表現
行と列のインデックスをもつ通常の表は次に記載の手順で表現できます (図 3 を参照)。
Step 1. 横向きにした 2 本の直線を上下に用意し、それぞれの直線を行と列に対応させます。 Step 2. それぞれの直線にインデックスに対応した点をそれぞれ描画します。 Step 3. 2 本の直線にある点の間を線で結ぶと、その線が「通常の表」における「セル」に対応します。
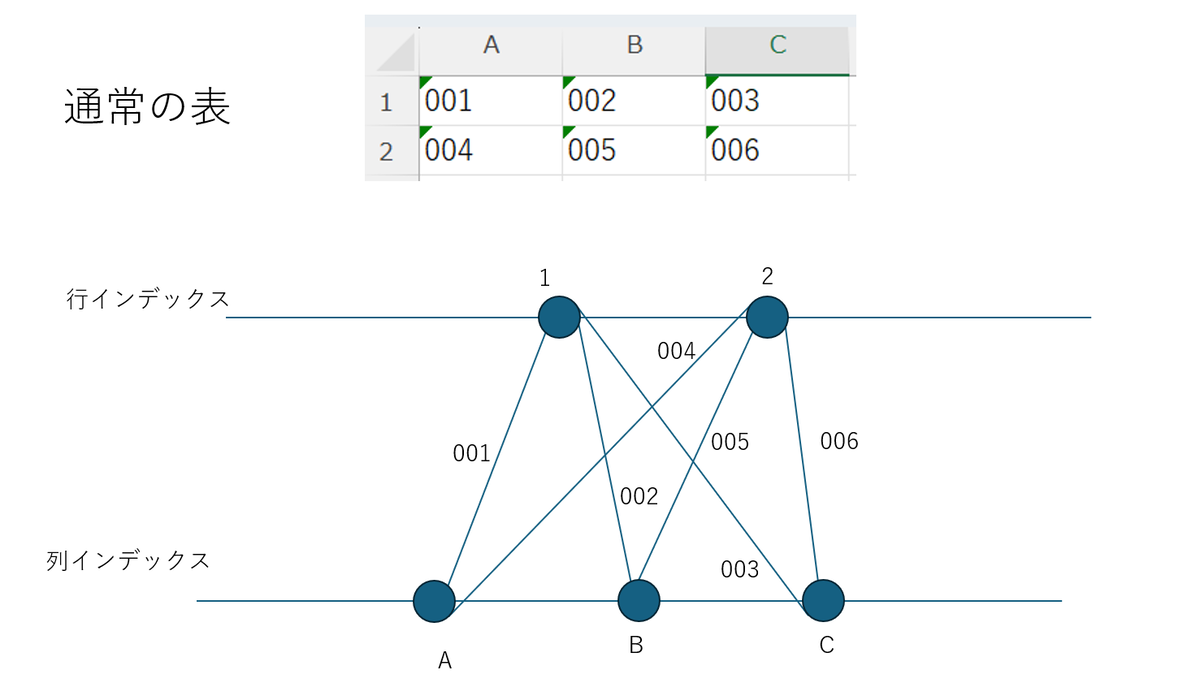図 3. 表の別表現
「マルチインデックスをもつ表」の別表現
マルチインデックスをもつ表は次に記載の手順で表現できます (図 4 を参照)。
Step 1. 2 個のハイパーキューブを上下に用意し、それぞれのハイパーキューブを複数行と複数列に対応させます。 Step 2. それぞれのハイパーキューブにインデックスに対応した点をそれぞれ描画します。 Step 3. 2 個のハイパーキューブにある点の間を線で結ぶと、その線が「マルチインデックスをもつ表」における「セル」に対応します。
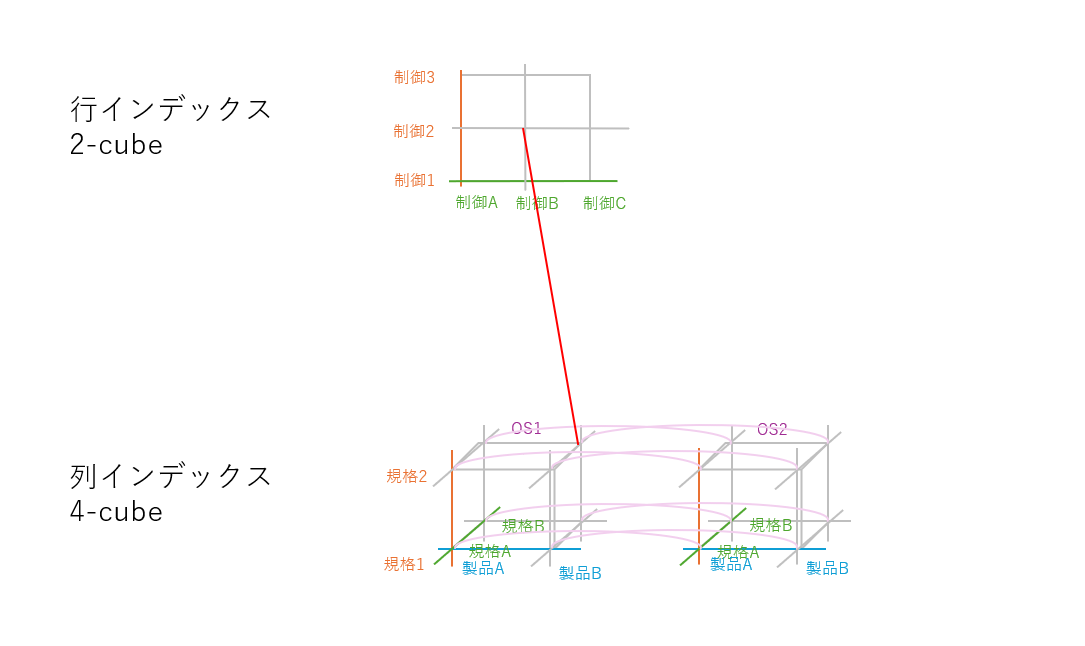図 4. マルチインデックスをもつ表の別表現。赤い線が図 1 の赤いセルと対応します。
課題
マルチインデックスをもつような表をエクセルファイル台紙として作成するシーンが業務上であります。
例えば、図1 におけるマルチインデックスがより多い場合を考えます。
- 行インデックス: 「制御 1～5」の 5 種類、「制御 A～E」の 5 種類としたとき、5 * 5 = 25 通り。
- 列インデックス: 「機種種別α」が 5 種類、「機種種別β」が 5 種類、「製品の種別」が 3 種類、「OS 種別」が 2 種類としたとき、5 * 5 * 3 * 2 = 150 通り。
上記に記載のような「マルチインデックスをもつ表」を組合せの誤りなく作成しようとすると、チェックも含めて 1 時間以上はかかると考えられますが、こちらが最小限のデータ入力のみで数分で可能になります。
ツールによる解決
マルチインデックスをもつ表を構造としてきれいに取り扱うために、そのインデックスをハイパーキューブとして捉え、マルチインデックスをもつ表の作成ツールを作成しました。
特徴
- Streamlit と呼ばれる Python モジュールにより作成。
- 行インデックスと列インデックスにそれぞれ対応するハイパーキューブを 3 次元に埋め込んで描画。
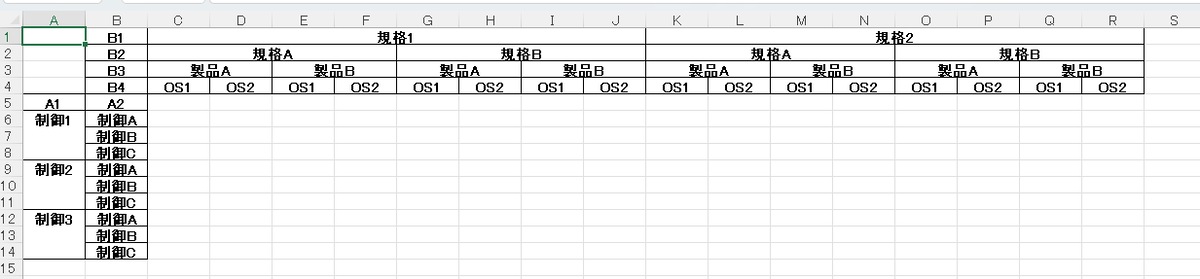図 5. ツールから出力したエクセルファイル。
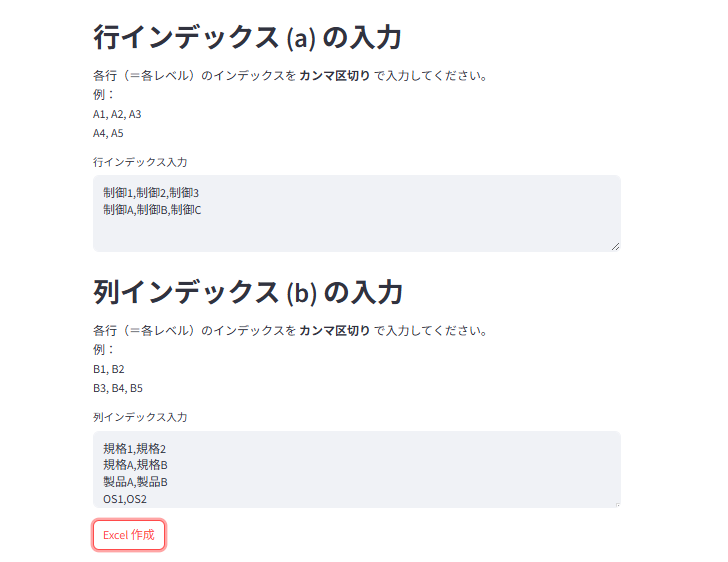図 6. マルチインデックスを入力。それぞれカンマ区切りで改行します。
図 7. ハイパーキューブを描画。行インデックスは 4-cube ですが、図 2 の 4-cube とは異なった描画をしています。
ソースコード
MOTEX 社内の AI サービスと相談しながら作成しました。所要時間は生成と微調整で 30 分ほどです。
import streamlit as st import pandas as pd import numpy as np import io import itertools import plotly.graph_objects as go st.title("マルチインデックス作成＆ハイパーキューブ 3D プロットツール") st.markdown(""" 【使い方】 ・下記「行インデックス (a) の入力」と「列インデックス (b) の入力」において、 各レベル（軸）ごとにインデックス文字列を**カンマ区切り**で入力してください。 例）行側に A1, A2, A3 A4, A5 と入力すれば、１軸目は 3 トークン、２軸目は 2 トークンとなります。 ・Excel 用の表は全トークンの直積となりますが、3D プロット用は 各軸は入力されたトークン数分の点が「辺上に均等配置」され、各点に対応するラベルが付与されます。 ※ レベル数に制限は設けていません. """) st.markdown("## 行インデックス (a) の入力") st.markdown(""" 各行（＝各レベル）のインデックスを **カンマ区切り** で入力してください。 例： A1, A2, A3 A4, A5 """) a_input = st.text_area("行インデックス入力", height=100) st.markdown("## 列インデックス (b) の入力") st.markdown(""" 各行（＝各レベル）のインデックスを **カンマ区切り** で入力してください。 例： B1, B2 B3, B4, B5 """) b_input = st.text_area("列インデックス入力", height=100) # ───────────────────────────── # Excel 作成と MultiIndex 表の作成（Excel は変更せず） # ───────────────────────────── if st.button("Excel 作成"): # 各テキストエリアを改行で分割（全レベル） a_lines = [line for line in a_input.splitlines() if line.strip()] b_lines = [line for line in b_input.splitlines() if line.strip()] # 各行をカンマで分割（全トークン）＆前後の空白除去 a_levels_full = [ [token.strip() for token in line.split(",") if token.strip()] for line in a_lines ] b_levels_full = [ [token.strip() for token in line.split(",") if token.strip()] for line in b_lines ] # Excel 用 MultiIndex は、各レベルの全要素の直積 try: row_index = pd.MultiIndex.from_product( a_levels_full, names=[f"A{i+1}" for i in range(len(a_levels_full))] ) col_index = pd.MultiIndex.from_product( b_levels_full, names=[f"B{i+1}" for i in range(len(b_levels_full))] ) except Exception as e: st.error("MultiIndex の作成に失敗しました。入力形式を確認してください。") st.stop() # DataFrame は、各セルを空文字で埋める例 df = pd.DataFrame("", index=row_index, columns=col_index) st.subheader("【生成された MultiIndex DataFrame のイメージ】") st.dataframe(df) # Excel 出力（in-memory） output = io.BytesIO() with pd.ExcelWriter(output, engine="xlsxwriter") as writer: df.to_excel(writer, sheet_name="MultiIndex") output.seek(0) st.download_button( label="Excel ファイルをダウンロード", data=output, file_name="multi_index.xlsx", mime="application/vnd.openxmlformats-officedocument.spreadsheetml.sheet" ) # ───────────────────────────── # 3D プロット用のハイパーキューブ作成 # ここでは、描画用には各軸は入力された全トークンをそのまま利用します。 # ───────────────────────────── a_levels_plot = a_levels_full b_levels_plot = b_levels_full def draw_hypercube(level_tokens, title="Hypercube"): # level_tokens : 各軸ごとのトークンリスト（例：[['A1','A2','A3'], ['A4','A5']]) d = len(level_tokens) if d < 1: st.error("ハイパーキューブのレベル（軸）がありません。") return None # 各次元 i に対して、3D 空間内での基底ベクトルを定義する basis = [] for i in range(d): angle = 2 * np.pi * i / d z = (i - (d - 1) / 2) / d basis.append(np.array([np.cos(angle), np.sin(angle), z])) basis = np.array(basis) # shape (d, 3) # ハイパーキューブの頂点は各次元が 0 または 1 の組み合わせ（tuple） vertices_bin = list(itertools.product([0, 1], repeat=d)) vertices = [] for v in vertices_bin: v_arr = np.array(v) point = np.dot(v_arr, basis) vertices.append(point) vertices = np.array(vertices) # shape (2^d, 3) # edges 用の描画リスト base_line_x, base_line_y, base_line_z = [], [], [] edge_line_x, edge_line_y, edge_line_z = [], [], [] # 各辺を描画（各頂点 v から、v[i]==0 の場合に隣接頂点 v2 へ） for v in vertices_bin: v = list(v) v_idx = vertices_bin.index(tuple(v)) p0 = vertices[v_idx] for i in range(d): if v[i] == 0: v2 = v.copy() v2[i] = 1 try: idx2 = vertices_bin.index(tuple(v2)) except ValueError: continue p1 = vertices[idx2] # 基底の細い灰色線（両端点を結ぶ） base_line_x.extend([p0[0], p1[0], None]) base_line_y.extend([p0[1], p1[1], None]) base_line_z.extend([p0[2], p1[2], None]) # 各軸 i のトークン数分（最低2点）の直線上サンプル k = len(level_tokens[i]) if len(level_tokens[i]) >= 2 else 2 for t in np.linspace(0, 1, k + 2)[1:-1]: pt = p0 + (p1 - p0) * t edge_line_x.append(pt[0]) edge_line_y.append(pt[1]) edge_line_z.append(pt[2]) edge_line_x.append(None) edge_line_y.append(None) edge_line_z.append(None) fig = go.Figure() # ① 基底エッジ（太さは控えめ）を描画 fig.add_trace(go.Scatter3d( x=base_line_x, y=base_line_y, z=base_line_z, mode="lines", line=dict(color="gray", width=1), name="Base Edges" )) # ② 各辺上のトークン配置線を描画 fig.add_trace(go.Scatter3d( x=edge_line_x, y=edge_line_y, z=edge_line_z, mode="lines+markers", marker=dict(size=1, color="gray"), line=dict(color="gray", width=4), name="Edges" )) # ───────────────────────────── # ③ グリッド線（Token Grid）の描画 # 原点は (0,…,0) に対応する頂点（vertices_bin の先頭要素） origin = vertices[vertices_bin.index((0,)*d)] # 各軸ごとに、原点からその軸方向の頂点までの差分ベクトル diff[i] を求める diff_vectors = [] for i in range(d): v1 = [0]*d v1[i] = 1 idx_v1 = vertices_bin.index(tuple(v1)) p1 = vertices[idx_v1] diff_vectors.append(p1 - origin) diff_vectors = np.array(diff_vectors) # shape (d, 3) # 各軸毎の token 配置パラメータ T[i]（(0,1)内の token の位置） T = [] for i in range(d): token_count = len(level_tokens[i]) if len(level_tokens[i]) >= 2 else 2 T.append(np.linspace(0, 1, token_count+2)[1:-1]) # 既存のグリッド線の描画（各軸方向に他軸固定値との直積で線分生成） grid_line_x, grid_line_y, grid_line_z = [], [], [] num_points = 10 # グリッド線上の補間点数 for i in range(d): fixed_axes = [j for j in range(d) if j != i] if fixed_axes: fixed_values_product = itertools.product(*(T[j] for j in fixed_axes)) else: fixed_values_product = [()] # d==1 の場合 for fixed_values in fixed_values_product: fixed_sum = np.zeros(3) for idx, j in enumerate(fixed_axes): fixed_sum += fixed_values[idx] * diff_vectors[j] # 軸 i 方向のパラメータを変化させる線分を生成 for t in np.linspace(0, 1, num_points): pt = origin + fixed_sum + t * diff_vectors[i] grid_line_x.append(pt[0]) grid_line_y.append(pt[1]) grid_line_z.append(pt[2]) grid_line_x.append(None) grid_line_y.append(None) grid_line_z.append(None) fig.add_trace(go.Scatter3d( x=grid_line_x, y=grid_line_y, z=grid_line_z, mode="lines", line=dict(color="lightgray", width=1), name="Token Grid" )) # ───────────────────────────── # ⑥ 格子点（各 token の組み合わせ）の座標をホバー表示するための散布図 # 各格子点の位置は、原点 + 各軸の token パラメータの直積により計算 grid_points_x = [] grid_points_y = [] grid_points_z = [] grid_hovertexts = [] # 軸ごとの色（トークン部分の色） axis_colors = ["red", "blue", "green", "orange", "purple", "brown", "magenta", "cyan"] # 各軸の token 数 token_counts = [len(T[i]) for i in range(d)] for indices in itertools.product(*[range(n) for n in token_counts]): pos = origin.copy() for i, idx in enumerate(indices): pos = pos + T[i][idx] * diff_vectors[i] grid_points_x.append(pos[0]) grid_points_y.append(pos[1]) grid_points_z.append(pos[2]) # ホバー表示用テキストを作成 hover_text = "<span style='color:black'>(</span>" for i, idx in enumerate(indices): if i > 0: hover_text += "<span style='color:black'>, </span>" token_str = level_tokens[i][idx] token_color = axis_colors[i % len(axis_colors)] hover_text += f"<span style='color:{token_color}'>{token_str}</span>" hover_text += "<span style='color:black'>)</span>" grid_hovertexts.append(hover_text) fig.add_trace(go.Scatter3d( x=grid_points_x, y=grid_points_y, z=grid_points_z, mode="markers", marker=dict(size=4, color="rgba(0,0,0,0)"), # マーカーは見えない hoverinfo="text", hovertext=grid_hovertexts, name="Grid Points", hovertemplate="%{hovertext}<extra></extra>" )) # ───────────────────────────── # ④ 各頂点を描画 fig.add_trace(go.Scatter3d( x=vertices[:, 0], y=vertices[:, 1], z=vertices[:, 2], mode="markers", marker=dict(size=2, color="black"), name="Vertices" )) # 軸ごとのカラーパレットは既に axis_colors を使用 # ⑤ 代表軸の辺上に各サンプル点（トークン）のラベルを追加 annotations = [] for i in range(d): tokens = level_tokens[i] # 代表軸: 原点から、i 番目の軸方向 v0 = [0] * d v1 = v0.copy() v1[i] = 1 idx0 = vertices_bin.index(tuple(v0)) idx1 = vertices_bin.index(tuple(v1)) p0 = vertices[idx0] p1 = vertices[idx1] k = len(tokens) if len(tokens) >= 2 else 2 sample_pts = [p0 + (p1 - p0) * t for t in np.linspace(0, 1, k + 2)[1:-1]] label_color = axis_colors[i % len(axis_colors)] for pt, token in zip(sample_pts, tokens): annotations.append(dict( x=pt[0], y=pt[1], z=pt[2], text=token, showarrow=False, font=dict(color=label_color, size=24), xanchor="center", yanchor="middle" )) fig.update_layout( title=title, scene=dict( annotations=annotations, xaxis_title="X", yaxis_title="Y", zaxis_title="Z" ), margin=dict(l=0, r=0, t=40, b=0) ) return fig # 行側と列側のハイパーキューブをそれぞれ描画（入力されたトークンをそのまま利用） fig_a = draw_hypercube(a_levels_plot, title="Row Index Hypercube") fig_b = draw_hypercube(b_levels_plot, title="Column Index Hypercube") st.subheader("【3D プロット：行インデックス側のハイパーキューブ】") if fig_a is not None: st.plotly_chart(fig_a, use_container_width=True) st.subheader("【3D プロット：列インデックス側のハイパーキューブ】") if fig_b is not None: st.plotly_chart(fig_b, use_container_width=True)
終わりに
- マルチインデックスをもつエクセルファイル作成をしようとすると、膨大な多重のインデックスを手動で作成する必要があります。
- 上記を本ツールを用いて省力化できます。
- 参考にした [m-hiyama-second.hatenablog:20210127] では、行インデックスと列インデックスがともに 2-cube の例が書かれています。
- また、ツールの本質的には表の出力ができれば十分ではありますが、マルチインデックスのハイパーキューブ描画もやってみました！
開発・品質管理問わず種々の業務において、マルチインデックスをもつ表を作成することがあれば参考になると幸いです。
お読みいただきありがとうございました。
